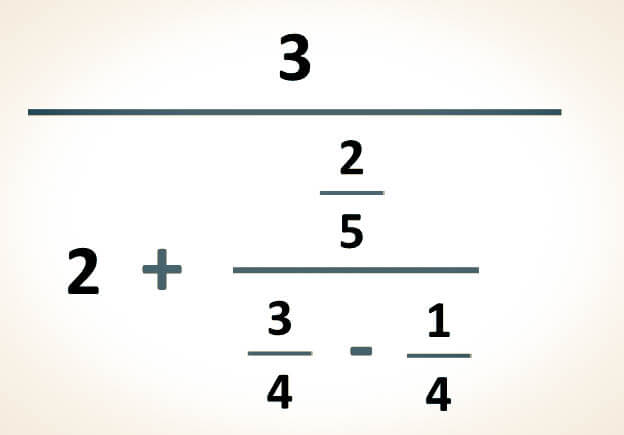Descubre nuestra metodología para aprender Aritmética

La aritmética es la rama de las matemáticas dedicada al estudio de los números y las operaciones básicas que se realizan con ellos, como la suma, la resta, la multiplicación y la división. Se centra en cálculos concretos y exactos, constituyendo la base para comprender y desarrollar otros campos matemáticos.

Ejemplo

-Resuelve la siguiente expresión aplicando la jerarquía de operaciones:

2 x 10 + 5 = 25

El álgebra, por otro lado, es la rama de las matemáticas que utiliza símbolos y letras para representar números y cantidades. Esto permite generalizar operaciones y relaciones, facilitando la formulación y solución de ecuaciones, así como el análisis de patrones y estructuras de forma abstracta. Su enfoque va más allá del cálculo directo, permitiendo modelar problemas complejos de manera general.

Ejemplo

-Resuelve la siguiente ecuación con una incógnita:

2y + 5 = 25


2y = 25 - 5


2y = 20


y = 20 ÷ 2


y = 10

En resumen, mientras la aritmética se enfoca en operaciones numéricas concretas, el álgebra amplía estos conceptos a través de la abstracción, permitiendo un análisis más profundo y general de las relaciones matemáticas.

-Fundamentos

Comienza por lo básico: Familiarízate con el concepto de número y sus diferentes clasificaciones.

Profundiza en las propiedades: Explora las características de los números naturales, decimales y fraccionarios.

Domina las operaciones básicas: Antes de aprender los algoritmos, asegúrate de comprender el significado de sumar, restar, multiplicar y dividir.

Comprende las operaciones: Aprende qué operaciones son válidas para cada tipo de número. Recuerda que el conjunto numérico puede influir en la posibilidad de realizar una operación, por ejemplo:

-Esta sustracción no puede realizarse con números naturales:

3 - 4 =

-Pero sí dentro del conjunto de los números enteros:

3 - 4 = -1

-Estrategias de aprendizaje

Aplica la clasificación semántica: Dale un significado a cada contenido y relaciónalo con otros temas para una mejor comprensión.

Desarrolla tu lógica: Combina la lógica con los conceptos aritméticos para resolver cualquier tipo de ejercicio.

-Hábitos de estudio

Sé autodidacta: Estudia por tu cuenta para mantenerte al día con los conocimientos requeridos en tu nivel escolar.

Refuerza tus conocimientos: Al pasar de primaria a secundaria, asegúrate de dominar al menos el 80% de la aritmética, ya que se asume un conocimiento previo en el alumno de nuevo ingreso.

-Dominio de las matemáticas

Conviértete en un experto: Desarrolla la habilidad de crear y resolver ejercicios en diversas variantes, así como poder identificar errores y clasificarlos correctamente.

-Práctica efectiva

Utiliza las herramientas disponibles: Emplea la calculadora, tutoriales y demás recursos para guiarte en la resolución de ejercicios. El objetivo es que logres resolverlos por ti mismo, primero con apoyo y luego de forma independiente.

Aplica el método declarativo: Enfócate en la lógica de resolución declarando el resultado del ejercicio sin detallar las operaciones. Utiliza la calculadora para obtener los resultados y evitar errores de cálculo, permitiéndote concentrar en el proceso de resolución y la secuencia de pasos.

Aprende a clasificar la información según su significado en seis categorías principales:

1. Tipos de números: Se exploran las diferentes clasificaciones de los números (naturales, enteros, racionales, irracionales, etc.) y sus propiedades fundamentales.

2. Conceptos y postulados: Se definen los principios básicos de la aritmética y se establecen los postulados que la rigen.

3. Operaciones: Se presentan las operaciones aritméticas, desde las básicas (suma, resta, multiplicación, división) hasta las más complejas (potenciación y radicación).

4. Simbología: Se introducen los símbolos matemáticos propios de la aritmética, facilitando su reconocimiento e interpretación dentro de las expresiones matemáticas.

5. Lógica: Se centra en analizar las relaciones entre cantidades, estableciendo si son iguales o distintas. Además, permite determinar la verdad o falsedad de proposiciones matemáticas y el reconocimiento de patrones.

6. Algoritmos: Se detallan los procedimientos paso a paso para la resolución de problemas específicos.

La clasificación semántica propuesta facilita la comprensión de bloques específicos de contenido dentro de un tema. Además, ayuda a organizar y dar sentido al aprendizaje, facilitando una comprensión más profunda y conectada.

Por ejemplo, el tema comúnmente abordado en clase, como la suma de fracciones, se entiende como un algoritmo que incluye la definición de los diferentes tipos de números que pueden sumarse y los métodos aplicables a cada caso.

37
+
17
=
47

Este tema, además, integra otros algoritmos relacionados, como la obtención del mínimo común múltiplo y el máximo común divisor, la conversión de fracciones y la suma de números. Asimismo, incorpora conceptos fundamentales, como el significado de sumar, la naturaleza de las fracciones y las partes que las componen.

5
+
2.75
+
34
+
125
=

La clasificación semántica propuesta también resulta útil para identificar y clasificar errores en la resolución de ejercicios matemáticos, como se muestra en los siguientes casos:

Solución correcta

"La suma de fracciones homogéneas (aquellas con el mismo denominador) se realiza sumando los numeradores y manteniendo el denominador. Si es posible, se simplifica la fracción resultante a su mínima expresión o se expresa como un número mixto o entero".

37
+
17
=
47

Soluciones incorrectas

Caso 1. El algoritmo empleado presenta un error al sumar linealmente los numeradores y los denominadores:

37
+
17
=
414

Caso 2. El algoritmo o la lógica de procedimiento son correctos, pero al sumar los numeradores se obtuvo un resultado incorrecto. Por lo tanto, el error se encuentra en la resolución de las operaciones básicas:

37
+
17
=
57

Caso 3. El error en este algoritmo radica en la incorrecta identificación de las partes de una fracción (numerador y denominador), ya que pasa igual los valores de los numeradores y suma los denominadores. El tipo de error en este caso es conceptual:

17
+
17
=
114

Caso 4. No se identifica el propósito del signo "+" en la operación, realizando una multiplicación en lugar de una suma:

37
+
17
=
37

Al aplicar esta metodología en la comprobación de ejercicios de matemáticas, facilita la identificación del tipo de error, ya sea algorítmico, conceptual, simbólico o relacionado con la resolución de operaciones básicas.

El estudio de la aritmética puede ser concebido como un entramado de temas interconectados, en lugar de una secuencia lineal de temas aislados. Esto implica que cada tema integra y depende de otros, formando una red de conceptos, postulados, algoritmos y lógica que se complementan entre sí.

Con base en este enfoque, a mayor número de conexiones entre los conocimientos involucrados en un tema, mayor será su nivel de dificultad para el aprendizaje.

Un claro ejemplo de esto es el estudio de las fracciones complejas, que a primera vista puede percibirse como un tema independiente. Sin embargo, dominarlo requiere comprender previamente una serie de conceptos relacionados, como la definición de fracción, sus partes, operaciones básicas, además de otros conocimientos relacionados.

Para abordar este problema de aprendizaje, la técnica sugerida dentro de esta metodología consiste en identificar los temas involucrados utilizando la clasificación semántica.

Aplicando esta metodología al caso de las fracciones complejas, su descomposición podría estructurarse de la siguiente manera:

Tipos de números: Identificar los tipos de números y fracciones implicados en el tema.

Conceptos y postulados: Comprender qué es una fracción, reconocer sus partes principales (numerador y denominador) y asimilar los postulados que rigen su simplificación, equivalencia y transformación.

Operaciones: Practicar las operaciones fundamentales con fracciones, como suma, resta, multiplicación y división, asegurando un dominio sólido de estas habilidades previas.

Simbología: Interpretar correctamente los símbolos matemáticos empleados en las fracciones complejas, como las barras de fracción y los operadores aritméticos.

Lógica: Determinar el orden de resolución de las operaciones contenidas en el numerador y el denominador.

Algoritmos: Los algoritmos necesarios para simplificar una fracción compleja son los siguientes:

• Suma, resta, multiplicación y división de fracciones y enteros. En la división de fracciones, es fundamental dominar tanto la división en forma horizontal como vertical, aplicando la conocida ley del sándwich.
• Conversión de números enteros, decimales y mixtos a sus respectivos números fraccionarios.
• Simplificación de fracciones.

En resumen, el aprendizaje de la aritmética es un proceso acumulativo: a medida que dominas más temas, puedes relacionar los nuevos conceptos con los ya aprendidos, facilitando y acelerando su comprensión. Al identificar la interconexión entre temas, permite mejorar la planificación curricular, adaptando el tiempo dedicado a cada tema según su complejidad y los conocimientos previos requeridos.