Resolver la raíz cuadrada de un número consiste en encontrar cuál es el número que multiplicado dos veces por sí mismo me da el valor del radicando.
Video
Ejemplo resuelto paso a paso, de una raíz cuadrada con tres cifras.
Sacar raíz cuadrada
¿Cómo calcular la raíz cuadrada?
Raíz cuadrada de 2 cifras
Para sacar la raíz cuadrada de un número de dos cifras, es necesario buscar un número del 1 al 9 que, al elevarse al cuadrado, dé como resultado el radicando de manera exacta o aproximada sin excederlo.
Ejemplos
Se puede afirmar que la raíz cuadrada de 16 es 4, debido a que al elevar 4 al cuadrado se obtiene como resultado el mismo valor que el radicando, es decir, 16.
√16 = 4
Comprobación
42 = 4 x 4 = 16
Por otro lado, se puede expresar que la raíz cuadrada de 38 es 6, dado que el número 6 elevado al cuadrado se aproxima al valor de 38 sin excederlo.
√38 = 6
Comprobación
62 = 6 x 6 = 36
Un numero entero positivo, tiene dos raíces cuadradas: una positiva y una negativa. Para indicar las dos raíces, se antepone el signo de más-menos al resultado.
Ejemplo
Se pueden expresar las dos raíces cuadradas del número 36 mediante el uso del signo de más-menos, como se muestra a continuación:
√36 = ± 6
Comprobación
62 = 6 x 6 = 36
(-6)2 = -6 x -6 = 36
Raíz cuadrada de 3 y 4 cifras
Para obtener la raíz cuadrada de un número de tres a cuatro cifras, se pueden seguir los siguientes pasos:
Paso 1. Se empieza dividiendo el radicando en grupos de dos cifras (de derecha a izquierda). Si el radicando tiene 3 cifras, el primer grupo tendrá dos cifras y el otro una sola.
Paso 2. Se debe obtener la raíz cuadrada del primer grupo de cifras (√10) y escribir el resultado (3) a un costado del radicando.
A continuación, se debe elevar al cuadrado el número anteriormente obtenido (32) y escribir debajo del primer grupo de cifras el resultado (9), para luego restarlo al grupo de cifras correspondiente.
Paso 3. Se bajan las cifras del grupo restante.
Paso 4. La raíz cuadrada obtenida hasta el momento (3), se multiplica por dos y el resultado (6) se escribe debajo de esta misma.
Paso 5. Una vez completado el paso anterior, se debe realizar una tabla de multiplicar del cero al nueve con factores iguales, donde al primer factor se le deberá anteponer la cifra escrita debajo de la raíz (6).
El objetivo será encontrar la multiplicación que dé como resultado el número conformado por el nuevo grupo de cifras (136), ya sea de forma exacta o aproximada.
Operaciones realizadas
60 x 0 = 0
61 x 1 = 61
62 x 2 = 124
63 x 3 = 189
64 x 4 = 256
65 x 5 = 325
66 x 6 = 396
67 x 7 = 469
68 x 8 = 544
69 x 9 = 621
El resultado de la multiplicación (124) debe escribirse debajo del grupo de cifras (136), mientras que la operación de multiplicación debe escribirse debajo de la raíz.
Paso 6. Finalmente, se debe realizar la resta del producto obtenido anteriormente (124) con el grupo de cifras correspondiente (136), para obtener el residuo de la raíz cuadrada (12). Luego, el factor utilizado (2) en la multiplicación del paso anterior se debe escribir en la parte correspondiente de la raíz cuadrada para completar el resultado final.
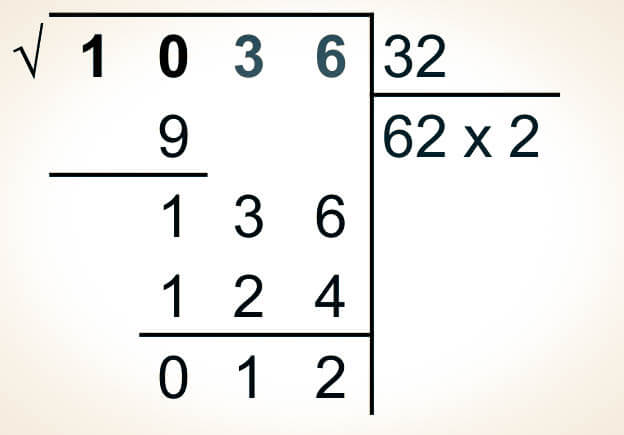
Raíz cuadrada de 5 y 6 cifras
Para obtener la raíz cuadrada de un número de cinco a seis cifras, se deben seguir los mismos pasos vistos anteriormente hasta llegar a la cuarta cifra. Luego, se debe seguir el siguiente procedimiento:
Se baja la primera cifra de la multiplicación (6) al siguiente renglón.
El segundo factor (2) se debe multiplicar por dos y luego escribir el resultado (4) en el siguiente renglón junto a la cifra anterior (6).
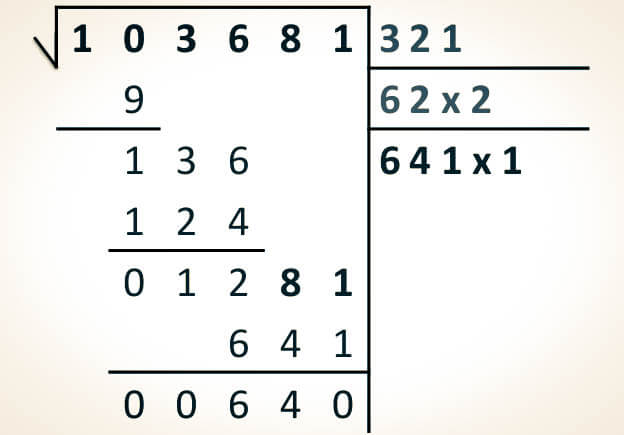
Una vez más, se bajan las cifras del último grupo (81) para conformar el número 1281.
Se desarrollan las tablas de multiplicar del cero al nueve, pero esta vez se antepone el número 64 al primer factor, con el objetivo de encontrar un número menor o igual a 1281.
La operación de multiplicación se escribe en el renglón correspondiente, al igual que el resultado, y por último se lleva el segundo factor (1) a la raíz cuadrada para obtener el resultado final.
