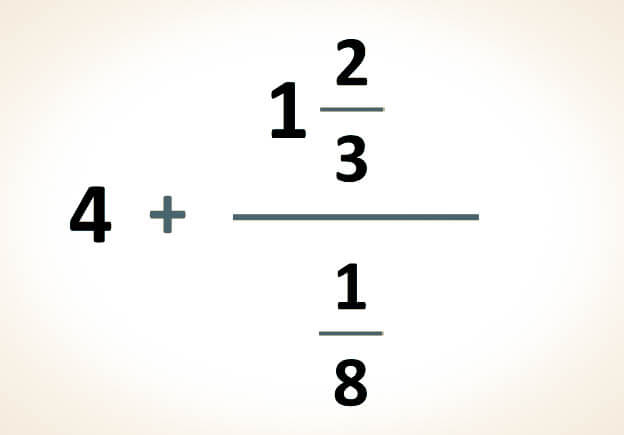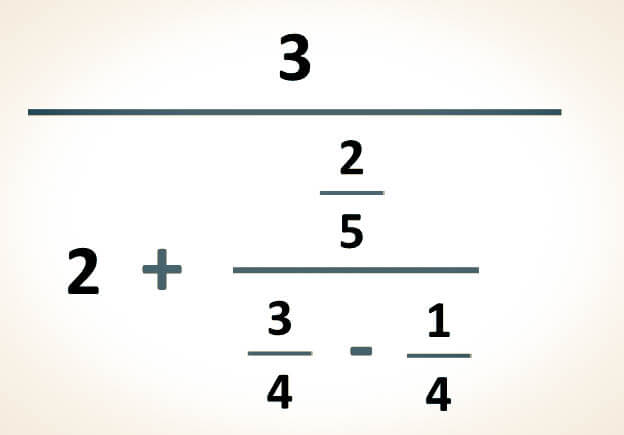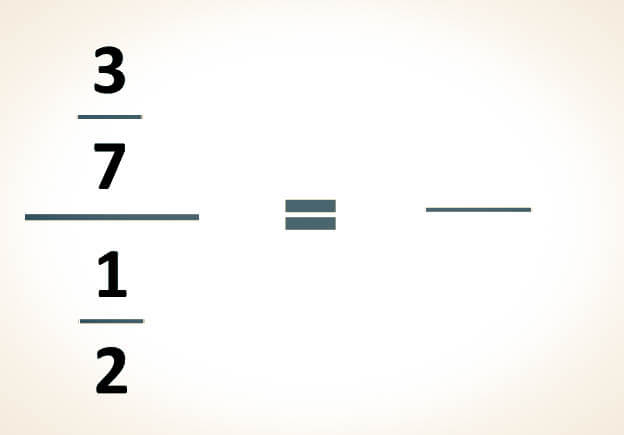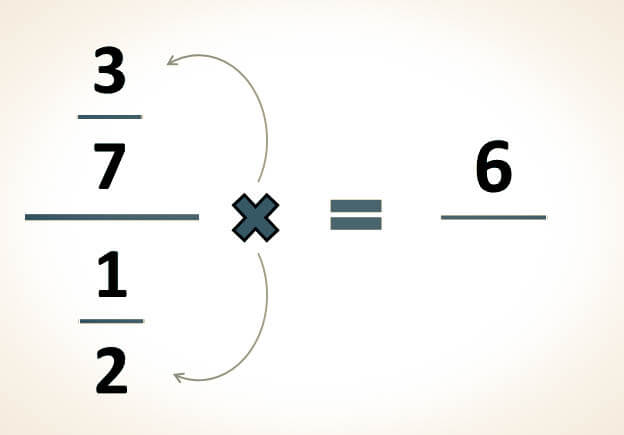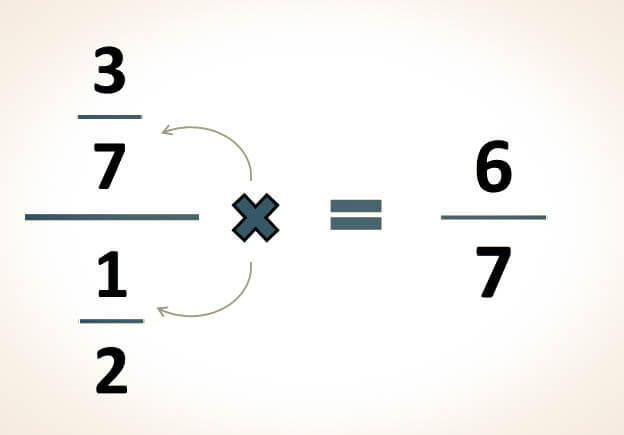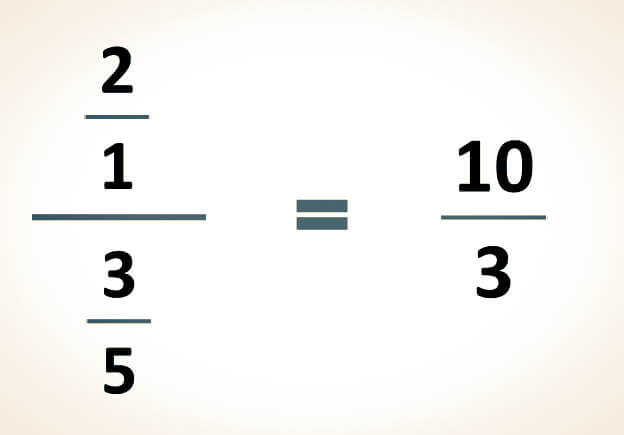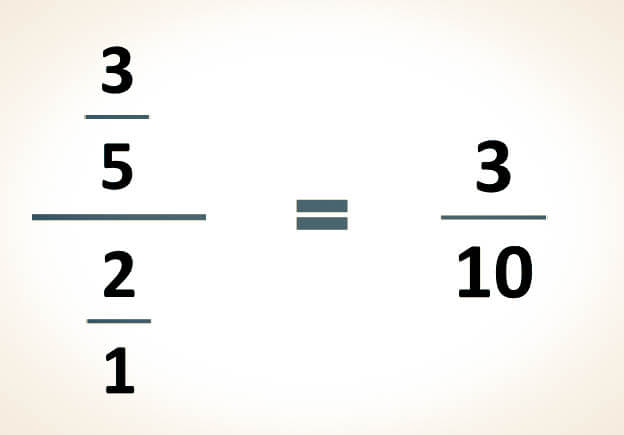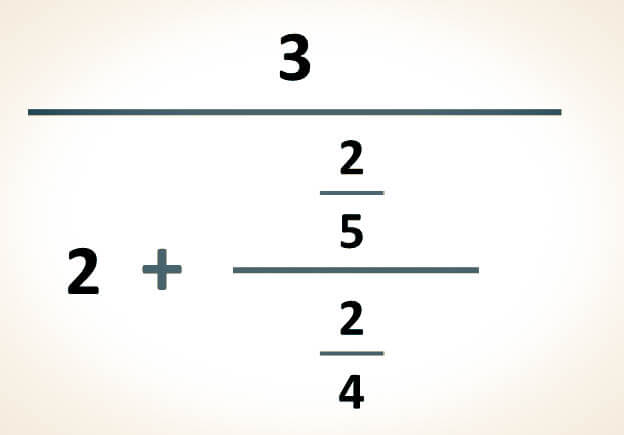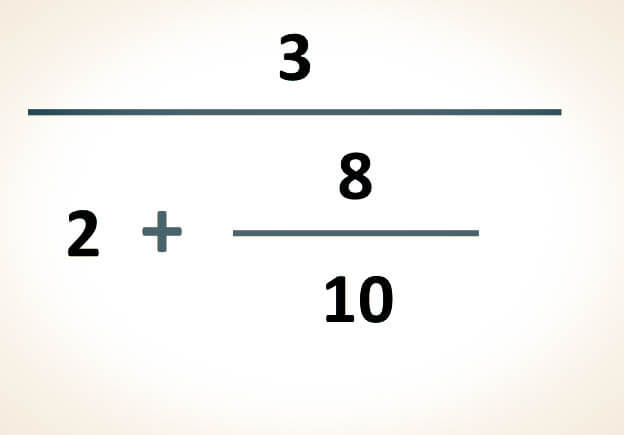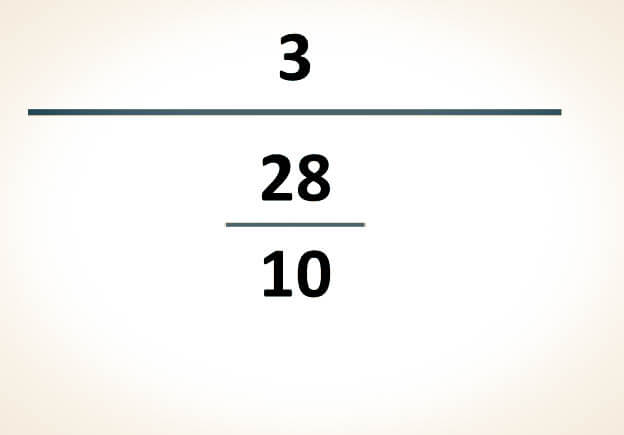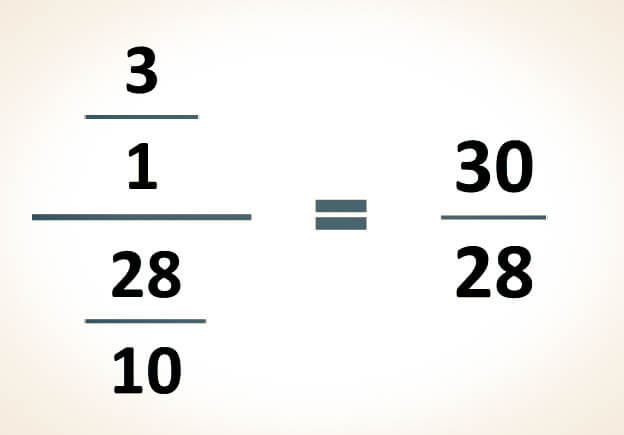Fracciones complejas

Una fracción compleja es una expresión en la que tanto el numerador como el denominador pueden contener fracciones, números enteros, decimales o números mixtos. El objetivo es simplificar esta expresión resolviendo todas las operaciones en el numerador y el denominador hasta obtener una fracción como resultado.

Ejemplo de una fracción compleja

Descripción

Resuelve operaciones con fracciones, números enteros, mixtos y decimales para ayudarte a simplificar una fracción compleja.

Datos permitidos

Símbolos matemáticos: Se permiten los siguientes símbolos de suma, resta, multiplicación, división y de agrupación.

+  -  x  /  (  )

Fracción: Se escribe como numerador : denominador

19
➔
1:9

Número mixto: Se escribe como entero e numerador : denominador

219
➔
2e1:9

Número entero

5

Número decimal

0.25

Ejemplo

-Para resolver la división vertical de la siguiente fracción compleja:

-Se debe introducir los siguientes datos en la calculadora:

1e2:3 / 1:8

-Una vez obtenido el resultado:

123
÷
18
=
403

-Puedes continuar resolviendo las operaciones restantes:

4
+
403

-Al ingresar los siguientes datos:

4 + 40:3

Los tipos principales de fracciones complejas son los siguientes:

1.- Fracción compleja en la que el numerador es un número entero y el denominador es una fracción.

2.- Fracción compleja en la que el numerador es una fracción y el denominador es un número entero.

3.- Fracción compleja en la que tanto el numerador como el denominador son fracciones comúnes.

4.- Fracción compleja conformada por otras fracciones y operaciones anidadas.

Para simplificar una fracción compleja, es fundamental determinar el tipo de expresión, ya que esto precisará el método a seguir:

Caso 1. Cuando una fracción compleja consta de una sola fracción tanto en el numerador como en el denominador, se requiere realizar una división vertical entre las dos fracciones.

Ejemplo

-Para simplificar la siguiente expresión, se aplica la conocida ley del sándwich:

-Primero se multiplican los extremos y se registra el producto como numerador:

-Luego, se multiplican los medios y el resultado se anota como denominador:

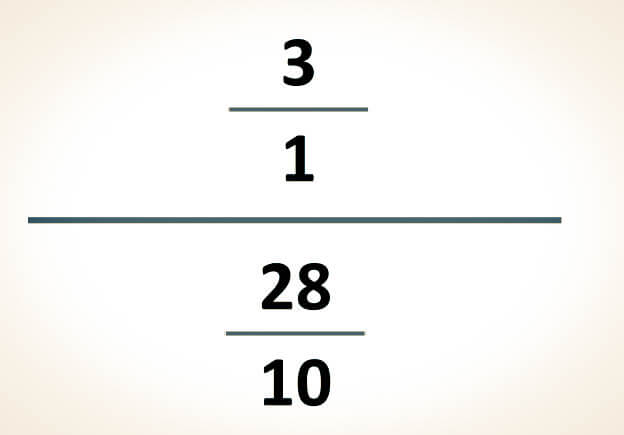
Caso 2. Cuando una fracción compleja está compuesta por un número entero y una fracción, es necesario transformar el número entero en una fracción. De esta manera, se podrá realizar la división de fracciones de forma vertical, tal como se explicó en el Caso 1.

Ejemplos

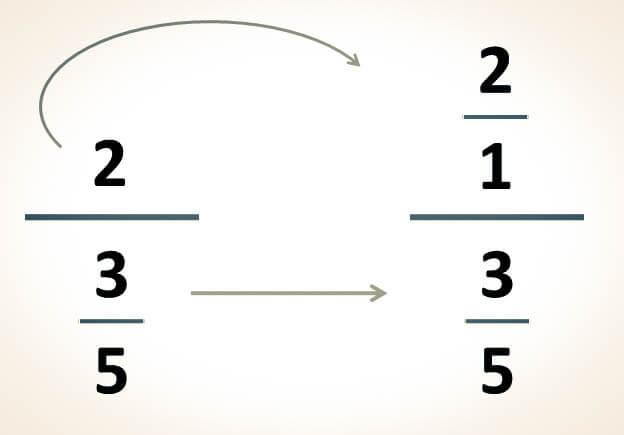
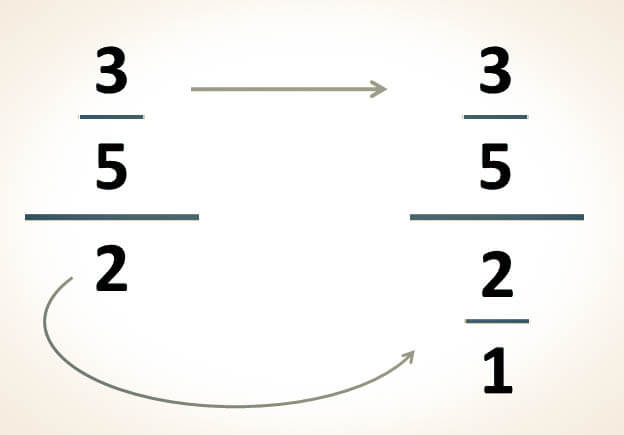
-Para simplificar las siguientes expresiones, el primer paso consiste en convertir el número entero en una fracción. Esta conversión se logra al colocar el número entero como numerador y el número 1 como denominador. Posteriormente, se debe resolver la división resultante para obtener la simplificación:

Ejemplo (A)

Resultado

Ejemplo (B)

Resultado

Caso 3. Para simplificar fracciones complejas con operaciones y fracciones anidadas, el orden de resolución se evalúa según el nivel de anidamiento.

Ejemplo

-Para simplificar la siguiente fracción compleja:

-Se inicia restando las fracciones para obtener el denominador de la división:

Operaciones

34
-
14
=
24

Sustitución

-Luego, se divide las fracciones aplicando la ley del sándwich:

Operaciones

25
÷
24
=
810

Sustitución

-Posteriormente, se suma el número entero a la fracción resultante:

Operaciones

2
+
810
=
2810

Sustitución

-El número entero ubicado en el numerador se convierte en fracción:

-Se realiza la última división vertical para simplificar la fracción compleja y obtener una fracción común:

-Finalmente, como el numerador y el denominador de la fracción resultante son divisibles entre 2, se simplifica a su mínima expresión:

3028
=
1514