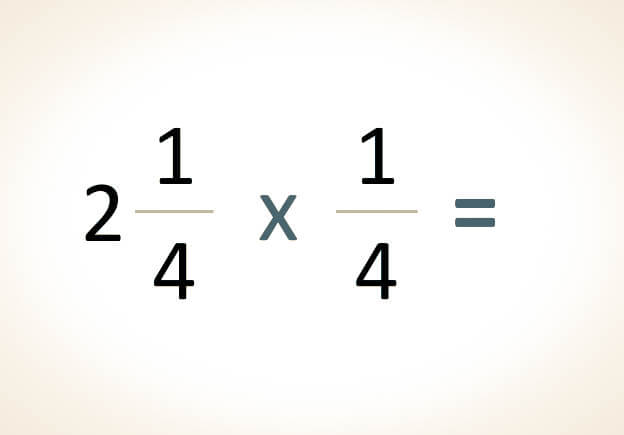Multiplicación de fracciones

La multiplicación de dos, tres o más fracciones se realiza mediante la multiplicación directa del numerador por numerador y del denominador por denominador. Posteriormente, se simplifica o reduce el resultado a su expresión más simple, siempre que sea factible.

Este método de resolución se aplica indistintamente, ya sea que las multiplicaciones tengan denominadores iguales o diferentes.

Ejemplo

La siguiente multiplicación consta de 3 fracciones comunes:

Como paso inicial, se debe multiplicar todos los numeradores, y el producto se coloca como numerador en una fracción resultante:

12
x
34
x
53
=
1 x 3 x 52 x 4 x 3
=
1524

Luego, se multiplican todos los denominadores y el producto se coloca como el denominador de la misma fracción resultante:

12
x
34
x
53
=
1 x 3 x 52 x 4 x 3
=
1524

Dado que tanto el numerador como el denominador son divisibles por 3, se simplifica la fracción para obtener el resultado:

12
x
34
x
53
=
1524
=
58

Para llevar a cabo la multiplicación entre una fracción y un número entero, el procedimiento consiste en primer lugar en convertir el número entero en una fracción común. Luego, se efectúa la multiplicación de manera lineal, multiplicando el numerador por el numerador y el denominador por el denominador.

Ejemplo

La siguiente multiplicación consta de un numero entero y una fracción:

Como primer paso, se transforma el número entero en una fracción, utilizando 3 como numerador y 1 como denominador:

Conversión

3

=

    
31

Sustitución

31
x
26

Posteriormente se multiplica el numerador por numerador y el denominador por denominador:

31
x
26
=
3 x 21 x 6
=
66

Finalmente, la fracción resultante puede simplificarse a términos más simples, ya que seis sextos equivalen a un entero:

31
x
26
=
66
=
1

Para llevar a cabo la multiplicación entre una fracción y un número mixto, el proceso implica, en primer lugar, la conversión de la fracción mixta en una fracción impropia. Una vez realizada esta conversión, se procede a llevar a cabo la multiplicación de fracciones de manera lineal.

Ejemplo

La siguiente multiplicación consta de un numero mixto y de una fracción común:

Como primer paso, se procede a la conversión del número mixto en una fracción impropia. Para lograrlo, se multiplica el denominador por el número entero y se le suma el valor del numerador. El resultado se registra en una nueva fracción como numerador, mientras que el denominador se mantiene igual al del número mixto:

Conversión

214
=
2 x 4 + 14
=
94

Sustitución

94
x
14

Posteriormente, se procede multiplicando numerador por numerador y denominador por denominador, obteniendo así el resultado de la multiplicación:

94
x
14
=
9 x 14 x 4
=
916

Para realizar la multiplicación entre una fracción y un número decimal, se debe comenzar con la conversión del número decimal en fracción decimal. Posteriormente se procede a multiplicar estas dos fracciones de forma lineal para obtener el resultado.

Ejemplo

La siguiente multiplicación consta de un numero decimal y una fracción común:

Para comenzar, se procede a convertir el número decimal en su fracción decimal equivalente. Para ello, se escribe como numerador el decimal prescindiendo del punto decimal y como denominador se escribe la unidad seguida de tantos ceros como cifras tenga la parte decimal:

Conversión

0.5
=
510

Sustitución

510
x
37

Luego, se procede a realizar la multiplicación de los numeradores y denominadores de manera lineal:

510
x
37
=
5 x 310 x 7
=
1570

Finalmente, dado que el numerador como el denominador de la fracción resultante son divisibles por 5, se procede a simplificar la fracción para obtener el resultado de la operación:

510
x
37
=
1570
=
314