Características del sistema de numeración decimal

El sistema de numeración decimal es un conjunto organizado de reglas y símbolos que permite representar y manipular cantidades numéricas. Este sistema define cómo se agrupan, ordenan y combinan los dígitos para expresar números, facilitando su comprensión y uso en operaciones matemáticas.

Las cifras, también conocidas como guarismos, son los signos utilizados para representar números. En el sistema de numeración decimal, se emplean las siguientes 10 cifras:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Se le denomina sistema decimal porque su base es 10. Esto significa que, al reunir diez unidades de un orden inferior, se forma una unidad en el orden inmediato superior.

Ejemplo

-La siguiente figura representa una unidad:

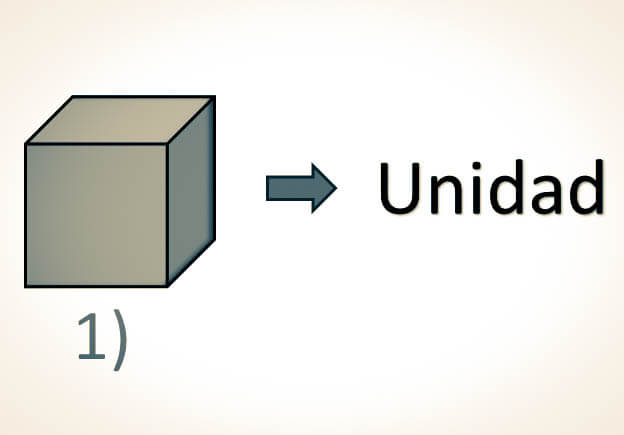
-Al reunir 10 unidades, se forma una decena:

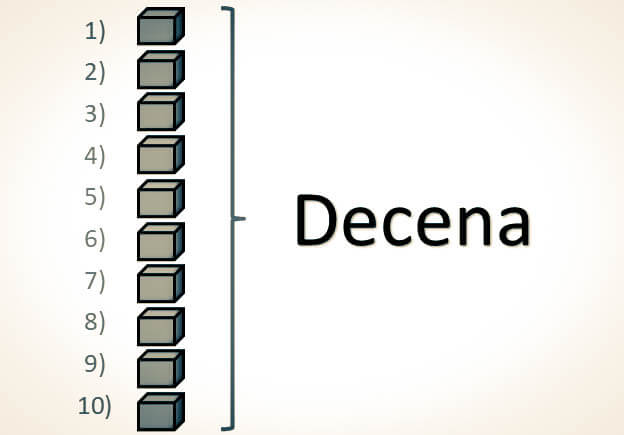
-Al agrupar 10 decenas (equivalentes a 100 unidades), se constituye una centena:

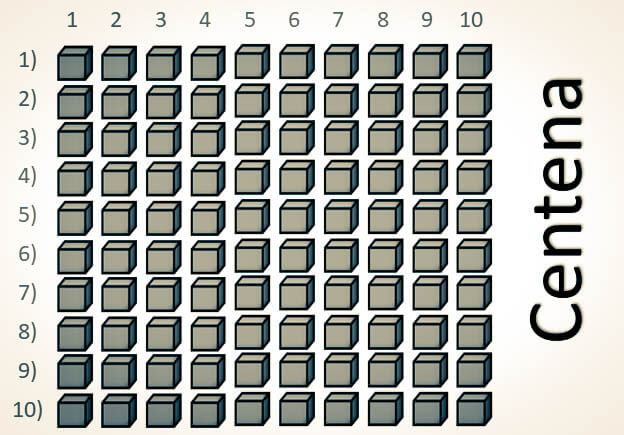
La generación de números se basa en la agregación de unidades, lo que permite establecer que la serie de los números naturales es infinita, ya que siempre se puede formar un nuevo número al sumar una unidad.

Bajo este principio, es posible representar una cantidad infinita de números utilizando un conjunto finito de signos o dígitos, en este caso, 10. Para ello se constituyen de forma lógica los números a partir de una cifra en adelante.

Ejemplos

-Números de una cifra:

1, 5, 9

-Números de dos cifras:

10, 25, 99

-Números de tres cifras:

650, 700, 999

En el sistema decimal, cada cifra tiene dos tipos de valores: el absoluto y el relativo.

El valor absoluto corresponde a la cantidad que representa la cifra por sí misma, independientemente de su posición.

Por otro lado, el valor posicional, también conocido como valor relativo, depende del lugar que ocupa la cifra dentro del número y está determinado por la posición que representa en la base 10. Es por ello, que el sistema decimal se clasifica como un sistema de numeración posicional.

Ejemplo

-El valor posicional de las cifras del número 3145 puede expresarse en notación desarrollada de las siguientes maneras:

3145 = 3 x 103  +  1 x 102  +  4 x 101  +  5 x 100

       
3145 = 3000 + 100 + 40 + 5

-Este número puede representarse en la siguiente tabla, permitiendo visualizar el orden al que pertenece cada una de sus cifras y determinar su valor posicional según la potencia de 10 correspondiente.

Procedimiento

3 x 103 = 3 x 1000 =  3000


1 x 102 = 1 x 100 =  100


4 x 101 = 4 x 10 =  40


5 x 100 = 5 x 1 =  5

La cifra cero, también conocida como cifra no significativa, es la única cuyo valor absoluto y posicional es igual a 0. Sin embargo, desempeña un papel fundamental en los números y tiene las siguientes propiedades:

1. Se utiliza para ocupar los lugares que carecen de unidades en un número, garantizando la correcta representación de su valor.

Ejemplo

500003

2. Representa la carencia de valor o un conjunto nulo cuando se encuentra sola o en posiciones específicas.

3. Uno o más ceros ubicados a la izquierda de una cifra significativa no incrementan el valor del número.

Ejemplo

0007 = 7

4. Uno o más ceros escritos a la derecha de una cifra significativa en números enteros incrementan el valor del número en potencias de 10.

Ejemplo

7000 = 7 x 103

5. En números decimales, los ceros ubicados a la derecha del último dígito significativo no alteran el valor.

Ejemplo

5.35000 = 5.35

6. Ceros a la izquierda de una cifra significativa en la parte decimal disminuyen su valor en potencias de 10.

Ejemplo

5.00035 < 5.035

El sistema decimal es un sistema de numeración posicional de base 10, por lo que utiliza 10 cifras distintas para representar los números. Su lógica de representación se desarrolla de la siguiente manera:

Números de una sola cifra:

Los primeros 10 números, del 0 al 9, corresponden a las unidades.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Números de dos cifras:

Para representar la siguiente secuencia de números, se combinan dos cifras: una que representa las decenas y otra que representa las unidades.

Se inicia con la primera cifra significativa (1), que ocupa el lugar de las decenas, y se combina con las cifras del 0 al 9:

10, 11, 12, 13, 14, 15, 16, 17, 18, 19

Al llegar al 9, se pasa a la siguiente cifra significativa (2) y se repite el mismo proceso:

20, 21, 22, 23, 24, 25, 26, 27, 28, 29

Este procedimiento continúa siguiendo el mismo patrón, hasta llegar al número 99.

Números de tres cifras:

Para representar la primera secuencia de números de tres cifras, se utiliza la tabla de números del 0 al 99 y se antepone la primera cifra significativa (1) al inicio de cada número. Esta cifra representaría a las centenas.

Si hay lugares que carecen de unidades, se agregan ceros para completar las tres cifras.

Por lo tanto, la secuencia numérica de los números de tres cifras comienza en el número 100 y finaliza en el número 999.

Este proceso ejemplifica cómo se generan las series numéricas, utilizando las secuencias anteriores para formar nuevas secuencias de mayor cantidad de cifras.

Para organizar grandes números y facilitar su lectura y escritura, el sistema decimal se estructura en:

• Órdenes: Cada una de las cifras dentro de una clase ocupa un orden. De derecha a izquierda, los órdenes son: unidades, decenas y centenas.
• Clases: Son grupos de tres cifras, separadas por comas o espacios. Cada clase representa una unidad distinta.
• Periodos: Un periodo está formado por dos clases consecutivas.

La siguiente tabla del sistema decimal ilustra cómo se agrupan los dos primeros periodos, indicando sus respectivas clases y órdenes.

Esta representación resulta especialmente útil para nombrar y escribir los números.

Abreviaturas

• U = Unidad
• D = Decena
• C = Centena
• M = Millar
• m = Millón

Ejemplo

El siguiente número está conformado por 12 cifras. Para facilitar su lectura, se agrupan las cifras de tres en tres, comenzando de derecha a izquierda. Esto permite identificar y nombrar las clases según corresponda.

Número escrito con cifras

583 290 074 416

Número escrito con letra

Quinientos ochenta y tres mil doscientos noventa millones setenta y cuatro mil cuatrocientos dieciséis

Los subórdenes se ubican a la derecha del punto decimal y se numeran de izquierda a derecha. En este suborden, cuanto más lejos esté una cifra del punto decimal, menor será su valor posicional.

Los subórdenes representan fracciones de una unidad. El primer suborden equivale a una décima parte de la unidad, el segundo a una centésima parte, el tercero a una milésima parte, y así sucesivamente.

La siguiente tabla del sistema decimal muestra los órdenes a la izquierda del punto decimal y los subórdenes a la derecha.

Ejemplo

El siguiente número decimal está formado por una parte entera (compuesta por una cifra) y una parte decimal (que contiene seis cifras). A continuación, se presenta la forma correcta de leer y escribir este número.

Número escrito con cifras

4.290036

Número escrito con letra

Cuatro enteros doscientos noventa mil treinta y seis millonésimos

A través de la tabla del sistema decimal, es posible determinar la equivalencia entre unidades de diferentes órdenes, como se ilustra a continuación:

Ejemplos

-¿Cuántas decenas hay en 7 decenas de millar?

7 DM = ? D

Para obtener esta equivalencia, se coloca el número 7 en la posición correspondiente a las decenas de millar y, a partir de ese orden, se añaden ceros hasta alcanzar el orden de las decenas. El número resultante representará la equivalencia buscada.

7 DM = 7000 D

De igual manera, esto aplica para los subórdenes del sistema decimal:

-¿Cuántos cienmilésimos hay en 6 décimos?

6 décimos = 60000 cienmilésimos