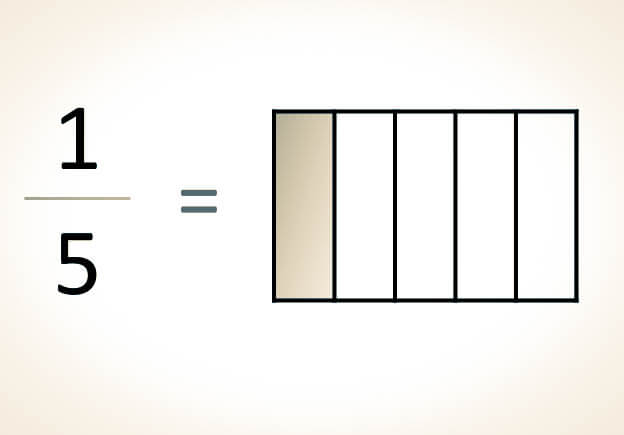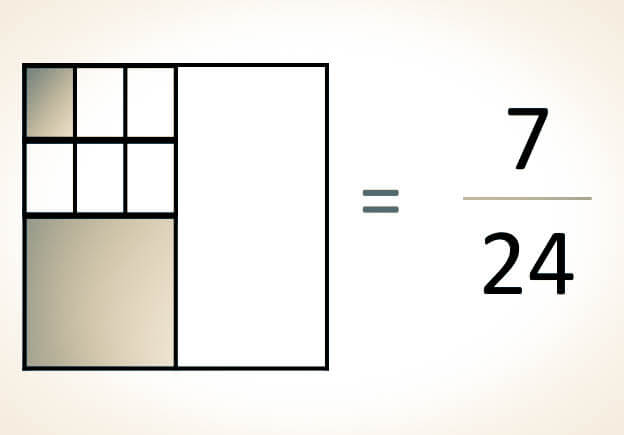Representación gráfica de fracciones

La representación gráfica de una fracción consiste en visualizarla mediante un dibujo o diagrama. Habitualmente, se divide una forma geométrica, en tantas partes iguales como indique el denominador y se sombrean las partes correspondientes al numerador. Esto permite comprender la fracción como una parte de un todo.

Para ilustrar una fracción, se pueden usar diversas formas geométricas como círculos, cuadrados, rectángulos y triángulos. No obstante, entre estas opciones, los cuadrados y rectángulos son particularmente útiles para dividir de manera más sencilla en partes iguales.

Los cuadrados son idóneos para representar fracciones con denominadores pares, como 2, 4, 6, 8 y 10.

En cambio, los rectángulos resultan ideales para visualizar fracciones con denominadores impares, como 3, 5, 7, 9 y 11.

Descripción

Representa de forma gráfica una fracción o un número mixto.

Datos permitidos

Fracción: Se escribe como numerador : denominador

19
➔
1:9

Número mixto: Se escribe como entero e numerador : denominador

219
➔
2e1:9

Ejemplo

-Para representar la siguiente fracción:

34

-Se ingresan los siguientes datos y finalmente, se oprime el botón Generar.

3:4

Al interpretar una figura geométrica para representarla como una fracción, se deben determinar los valores del numerador y del denominador. Para lograrlo, se lleva a cabo lo siguiente:

Paso 1. Se identifica el número total de partes iguales en que está dividida una sola figura completa; este valor se anota como el denominador.

Paso 2. Se cuenta la cantidad de partes sombreadas o coloreadas en la(s) figura(s), y este número se asigna como el numerador de la fracción.

Ejemplo

-En esta interpretación, el numerador es 4, ya que hay cuatro partes coloreadas, y el denominador es 3, porque cada figura está dividida en tres partes iguales.

Existen casos donde una figura se compone de secciones con diferentes tamaños, es decir, figuras que representan fracciones equivalentes contenidas unas dentro de otras.

Para interpretarlas correctamente, se debe identificar la sección de menor tamaño y usarla como referencia. Con base en esta sección, se determina en cuántas partes iguales de este menor tamaño se puede dividir la figura completa.

Este número será el denominador de la fracción. Posteriormente se cuentan cuantas de estas secciones de menor tamaño están sombreadas para así obtener el numerador.

Ejemplo

-En esta figura, un cuarto se divide en 6 partes iguales. Como una unidad tiene 4 cuartos, se multiplica 4 por 6, obteniendo 24 como denominador.

-Por otra parte, el numerador es 7, ya que de las 24 partes iguales, 7 están iluminadas.

Para representar fracciones mediante figuras geométricas, se realizan los siguientes pasos:

Paso 1. Determinar el total de figuras geométricas a dibujar.

Paso 2. Establecer en cuántas partes iguales se debe dividir cada figura.

Paso 3. Calcular el total de partes que deben ser coloreadas.

Consideraciones para cada tipo de fracción

NumeradorDenominador
=
Total de partes que se colorean.Partes iguales en que se divide la unidad.

Fracciones propias y unitarias: En estos casos, solo se requiere dibujar una figura geométrica. Esta figura se divide en partes iguales según lo que indique el denominador, y se colorea el número de partes que señale el numerador.

Ejemplos

-Para representar un cuarto, se dividió el cuadrado en 4 partes iguales y se sombreo una.

-Por otra parte, para representar cuatro cuartos, se dividió el cuadrado en 4 partes iguales y se sombreo todo el cuadrado, representando así la unidad.

Fracciones impropias: Para representar fracciones impropias, se divide el numerador entre el denominador para determinar la cantidad de figuras completas que se deben dibujar, considerando lo siguiente:

• Si el residuo de la división es cero, se dibujan tantas figuras como indique el cociente.
• Si el residuo es distinto de cero, se suma una unidad al cociente para determinar el total de figuras a dibujar.

Ejemplo

-Para representar la fracción siete cuartos, primero se divide el numerador entre el denominador:

-Como la división no es exacta, se suma una unidad al cociente, determinando así que se deben dibujar dos figuras:

1 + 1 = 2

-Finalmente, cada figura se divide en cuatro partes iguales, y se sombrean siete partes en total:

Números mixtos: Para la representación de números mixtos, primero se realiza la conversión a una fracción impropia. Luego, se sigue el procedimiento descrito para la representación de fracciones impropias.

134
=
74