Ubicar fracciones en la recta numérica

Las fracciones se representan en la recta numérica de manera similar a los números enteros. Para ello, se divide cada unidad en la recta en tantas partes iguales como indique el denominador de la fracción, y se cuentan dichas partes a partir del cero, hacia la derecha si la fracción es positiva, o hacia la izquierda si es negativa.

Ejemplo

-En la siguiente ilustración se muestra cómo se divide el primer segmento de recta en partes iguales, correspondientes al denominador de cada fracción:

-Posteriormente, se pueden enumerar las divisiones para ubicar las fracciones a partir de su numerador:

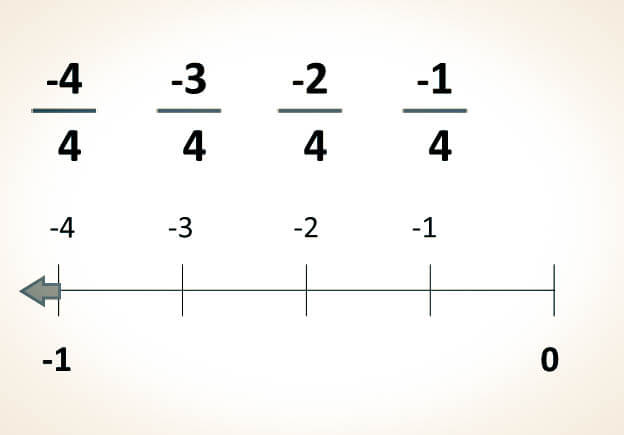
-Del mismo modo se representan las fracciones con signo negativo, solo que en sentido opuesto:

Observación

Dos o más fracciones equivalentes se deben ubicar en la misma posición de la recta numérica, una debajo de la otra, por ejemplo:

Para ubicar fracciones con diferentes denominadores en la recta numérica, se convierten primero en fracciones equivalentes con un denominador común.

Luego, se divide cada unidad de la recta en partes iguales según dicho denominador. Finalmente, se utiliza el numerador para posicionar cada fracción en la recta numérica.

Ejemplo

-Para ubicar las fracciones un medio y dos tercios en una misma recta numérica se realizan los siguientes pasos:

12
,
23

Paso 1. Se convierten dichas fracciones a un denominador común. Para ello, primero se calcula el mínimo común múltiplo (mcm) de los denominadores:

m.c.m = 2 x 3 = 6

Paso 2. Una vez obtenido el mcm, se establece como denominador común:

12
=
36

23
=
46

Paso 3. Se divide el común denominador entre el denominador de la fracción original y el resultado se multiplica por su numerador. Este resultado constituye el numerador de la fracción equivalente:

12
=
6 ÷ 2 x 16
=
36

23
=
6 ÷ 3 x 26
=
46

Paso 4. Se dibuja una recta numérica y cada unidad se divide en 6 partes iguales. Posteriormente, se ubica cada una de las fracciones en la recta, teniendo en cuenta el valor de sus numeradores:

Observación

Si se incluyen números mixtos, decimales y fracciones, por ejemplo:

0.5
,
123
,
14

Primero se deben convertir los números mixtos y decimales a sus fracciones equivalentes:

0.5
=
510
=
12

123
=
53

Posteriormente, con solo fracciones presentes:

12
,
53
,
14

Se procede a reducirlas a un común denominador como se mostró previamente, para poderlas representar en una misma recta numérica.