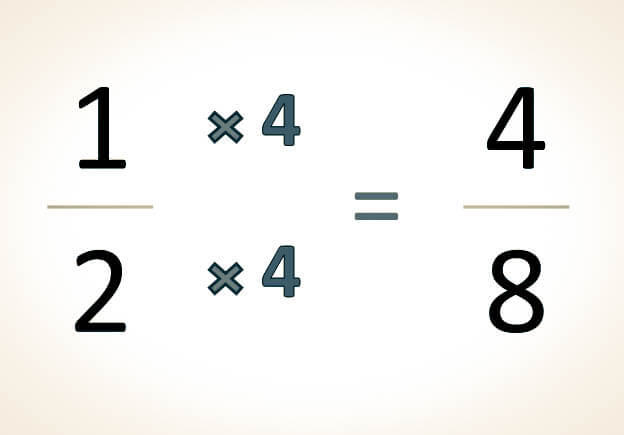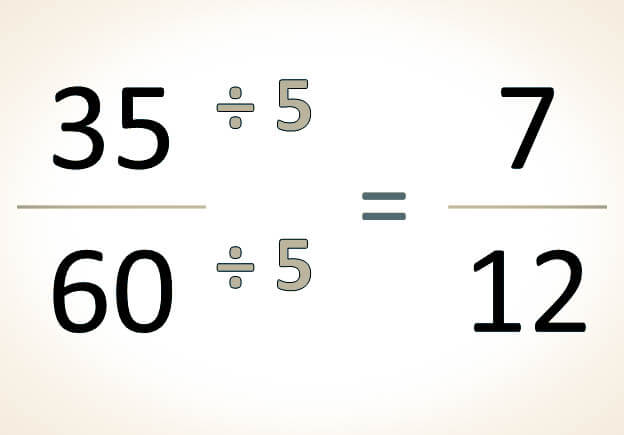Fracciones equivalentes

Se considera que dos o más fracciones son equivalentes cuando representan la misma proporción de la unidad, aun cuando sus numeradores y denominadores sean distintos.

Ejemplo

-En la ilustración que se presenta a continuación, se observan tres fracciones equivalentes, ya que todas representan la mitad de un entero.

Para verificar si dos fracciones son equivalentes, se utiliza la comprobación mediante productos cruzados.

Ejemplo

-Para determinar si las fracciones un medio y cuatro octavos son equivalentes, se aplica el método de los productos cruzados:

-Este método consiste en multiplicar el numerador de la primera fracción por el denominador de la segunda, y el denominador de la primera fracción por el numerador de la segunda:

Operaciones

1 x 8 = 8

2 x 4 = 8

-Dado que los productos resultantes son iguales, se concluye que las fracciones son equivalentes, lo cual se representa con el signo de igualdad:

Resultado

12
=
48

Para generar fracciones equivalentes cuyos términos (numerador y denominador) sean mayores o menores que los de una fracción dada, se pueden emplear dos métodos:

• Método de Amplificación.
• Método de Reducción y Simplificación.

Descripción

Genera fracciones equivalentes por amplificación o reducción.

Datos permitidos

Fracción: Se escribe como numerador : denominador

19
➔
1:9

Ejemplo

-Para obtener un listado de fracciones equivalentes dada la fracción:

2836

-Se ingresan los siguientes datos y finalmente, se oprime el botón Generar.

28:36

La amplificación de fracciones consiste en obtener una fracción equivalente a la original, pero con un numerador y un denominador de mayor valor.

Para amplificar una fracción, se multiplica tanto su numerador como su denominador por un mismo número entero mayor que 1.

Ejemplo

-La fracción un medio se puede amplificar multiplicando tanto el numerador como el denominador por 4. El resultado de esta operación es la fracción equivalente cuatro octavos.

Por otra parte, es posible amplificar una fracción en función de un denominador específico.

Ejemplo

-Para obtener la fracción equivalente de un medio en términos de doceavos, se realiza lo siguiente:

12
=
612

1. Se lleva a cabo la división del segundo denominador entre el primer denominador:

12 ÷ 2 = 6

2. Se toma el cociente obtenido (6) y se multiplica con el numerador de la primera fracción (1).

Resultado

12
=
1 x 612
=
612

La reducción de fracciones consiste en la obtención de una fracción equivalente, pero con términos de menor valor que los de la fracción original. Para lograrlo, se divide tanto el numerador como el denominador entre un divisor común que sea mayor que uno.

Ejemplos

-La fracción seis doceavos se puede reducir a términos menores, ya que tanto el numerador (6) como el denominador (12) comparten más de un divisor común.

612
=

Divisores del número 6

1, 2, 3, 6

Divisores del número 12

1, 2, 3, 4, 6, 12

Divisores en común

1, 2, 3, 6

-Por lo tanto, se puede elegir cualquier divisor común mayor que 1 para llevar a cabo la reducción:

Para reducir una fracción a otra equivalente con un denominador específico, se procede de la siguiente manera:

612
=
36

1. Se divide el denominador de la fracción original entre el denominador deseado. Este paso determina la relación de equivalencia entre las dos fracciones:

12 ÷ 6 = 2

2. El primer numerador se divide entre el resultado de la división previa para determinar el valor del segundo numerador:

6 ÷ 2 = 3

Resultado

612
=
36

La simplificación de fracciones consiste en la obtención de una fracción equivalente e irreducible; es decir, una fracción cuyo numerador y denominador sean números enteros con el mínimo valor posible.

Ejemplo

-Para simplificar la fracción treinta y cinco sesentavos, se realiza lo siguiente:

3560
=

1. Se obtiene el máximo común divisor (MCD) del numerador y el denominador de la fracción dada:

m.c.d(35,60) = 5

2. Se divide tanto el numerador como el denominador entre el MCD obtenido. El resultado de esta división dará lugar a la fracción equivalente irreducible:

Observación

No todas las fracciones pueden simplificarse a términos menores. Esto sucede cuando el numerador y el denominador son primos entre sí, es decir, cuando su único divisor común es el número 1. A estas fracciones se les denomina fracciones irreducibles.